26.11.2021
Pandemie der Placebo-Ungeimpften wäre denkbar
Von Julius Felix
Bei Corona könnte eine „Pandemie der Ungeimpften“ auch mit wirkungslosen Impfstoffen entstehen, wie eine britische Modellrechnung zeigt. Durch Meldeverzug entstehen andere Daten.
Im einem früheren Artikel wurde bereits über die „Pandemie der Ungeimpften“ aufgeklärt und wie diese Illusion unter anderem entsteht. Sehr spannend ist nun die mathematische Simulation, mit der die Professoren Martin Neil und Norman Fenton für großes, internationales Interesse sorgen: Was passiert, wenn ich einen Placebo-Impfstoff verimpfe, der die Sterblichkeit an der Krankheit überhaupt nicht verändert, aber trotzdem getrennte Zählungen für Geimpfte und Ungeimpfte durchführe?
Einer der Autoren, Prof. Fenton, ist ein britischer Mathematiker und kommuniziert die Ergebnisse über die sozialen Netzwerke. Er ist derzeit Professor für Risk Information Management an der Queen Mary University of London. Es geht bei dieser mathematischen Modellierung nicht darum, den Impfstoff madig zu machen, sondern sie zeigt, dass man eine „Pandemie der Ungeimpften“ sogar mit der Verimpfung von Kochsalzlösung bekäme, denn sie entsteht, sobald es einen Meldeverzug gibt, automatisch.
Er und sein Kollege Martin Neil, die auch diesen Blog-Artikel zusammen verfassten, hatten vor ein paar Monaten bereits für Aufsehen gesorgt, in dem sie erklärten, dass die britischen Daten zeigen würden, dass geimpfte Menschen häufiger stürben als ungeimpfte (auch nach Anpassung an das Alter). In diesem Beispiel beschäftigen sich die erfahrenen Mathematiker nun mit einem anderen Thema.
Rätselhafte Zahlen?
In dem Modell geht man von einer Population von 1.000.000 Menschen und einer Mortalitätsrate von 15 auf 100.000 Personen aus. Der Beobachtungszeitraum beträgt 20 Wochen, die Beobachtungsfrequenz eine Woche und liefert somit die Ergebnisse, die ein 7-Tages-Durchschnitt auch liefert. Betrachtet man die 20 Wochen bei einer Meldeverzögerung von 0, so ergibt sich für jede Woche eine Mortalitätsrate von 15 auf 100.000 Menschen.
Jetzt werden die Toten ja aber nicht tagesaktuell gemeldet – das weiß man auch vom RKI sowie anderen offiziellen Stellen in anderen Ländern. Was passiert nun bei einer realistischen Meldeverzögerung von zum Beispiel einer Woche? Es werden also die gleichen Toten gemeldet, aber eben eine Woche später, was bedeutet: Die Toten der alten Woche werden auf die jeweiligen Populationen der Folgewoche – geimpft und ungeimpft – angewendet. Wichtig ist hierbei zu betonen, dass die Woche ein Beispiel ist – jede realistische Meldeverzögerung, also Zeiteinheit wäre denkbar. Es müssen nicht sieben Tage sein, es könnten auch weniger sein.
„So entsteht dann mit einem Impfstoff, der real keinerlei Auswirkung auf die Mortalität hat, der Eindruck eines hochwirksamen Impfstoffes.“
Schauen wir uns das an einem Rechenbeispiel an (s. Abb. 1): In Woche 1 ohne Meldeverzögerung hat man einen Toten in der Gruppe von den 5000 Geimpften – Mortalitätsrate 15. Wenn man den Toten aber erst eine Woche später registriert, sind bereits mit dem in der Modellrechnung angenommenem Impftempo 9999 Menschen „vollständig geimpft“. Damit ist hier der Zeitpunkt gemeint, an dem der vollständige Impfschutz erreicht ist. So ergibt sich dann aber einer Mortalitätsrate von 7,5. Die ist aber falsch, weil sie ohne Meldeverzögerung bei 15 läge, denn der hypothetische Placebo-Impfstoff ändert ja nichts. In diesem Beispiel sieht man ein schnelles Fortschreiten der Impfung auf die Gesamtpopulation der Beispiel-Population. Das ist ein Unterschied zu den realen Impfkampagnen in den meisten Ländern, da am Ende des Zeitraums von 20 Wochen fast 100 Prozent der Bevölkerung geimpft sind. Eine solche Verkürzung ist üblich bei Beispiel-Modellen, die ein Prinzip verdeutlichen sollen.
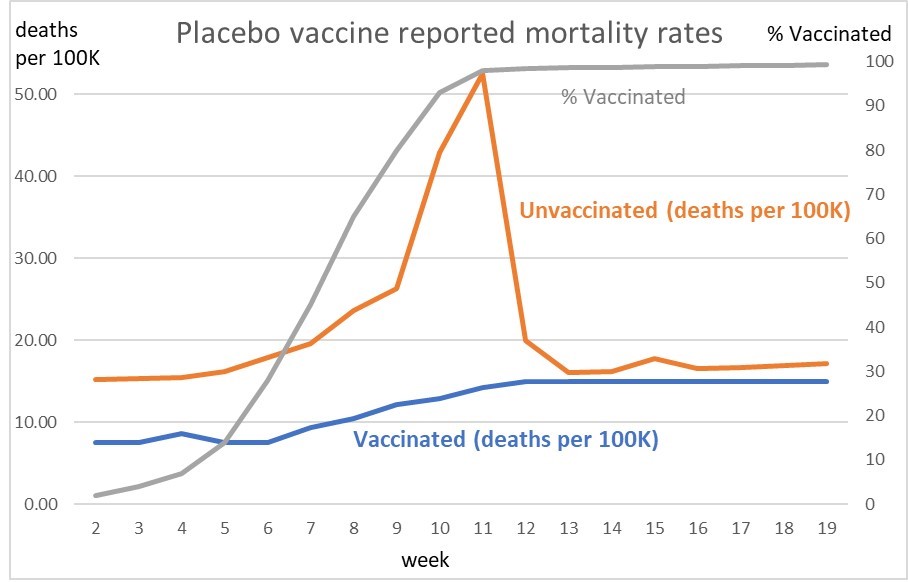
Abb. 1: Mortalitätsraten im mathematischen Modell, Quelle.
Durch dieses Phänomen sieht man über die 20 Wochen, wie sich die Mortalitätsrate unter den Geimpften den 15 – also der realen Rate – erst langsam wieder annähert, da ihre Population ja ansteigt durch die Impfungen. Bei den Ungeimpften sinkt die Population ja aber. Durch den gleichbleibenden Meldeverzug werden die alten hohen Todeszahlen auf eine immer weiter sinkende Population angewendet. Die Mortalitätsrate steigt also deutlich über 15 – in Woche 12 sogar bis auf über 52 und fällt dann in der Woche 13 auf 20 ab.
Anschließend sinkt sie weiter und nähert sich auch den 15 an, es normalisiert sich wieder, sodass wir letztendlich der Mortalitätsrate 15 in beiden Gruppen grob nahekommen. So entsteht dann mit einem Impfstoff, der real keinerlei Auswirkung auf die Mortalität hat, der Eindruck eines hochwirksamen Impfstoffes, weil der angeblich die Geimpften so toll schützt, da in der Gruppe ja scheinbar weniger sterben. Das tun sie aber gar nicht.
Diese Modellrechnung kann jeder in Excel nachbauen oder man schaut einfach auf die Tabellen im dazugehörigen Blogpost. Daran sieht man: Nur allein mit Verspätung von Daten – ob absichtlich oder nicht – kann man aus einem wirkungslosen Impfstoff einen „Gamechanger“ konstruieren. Man verimpft quasi ein Placebo wie in einer Kontrollgruppenstudie bei der Impfstoffzulassung. Daran ist nichts rätselhaft.
Vom Labor in die reale Welt
Wie immer bei Simulationen, die ein Prinzip verdeutlichen, kreiert man Idealbedingungen. Nun ist die reale Welt aber nicht ideal. Schaut man jedoch aber auf die Daten des Britischen Office of National Statistics (ONS) und des National Immunisation Management Systems (NIMS), konstatieren Fenton und Neil deutliche Ähnlichkeiten des Modells mit realen Entwicklungen in der Altersgruppe der 60-69jährigen.
Was machen die Autoren hier? Sie schauen sich die Mortalität außerhalb von coronaassoziierten Todesfälle der Geimpften und Ungeimpften an (s. Abb. 2). Hier muss die Sterblichkeit gleich bleiben, weil die Wahrscheinlichkeit auf Tod durch andere Krankheiten weder erhöht, noch verringert wird. Trotzdem sieht man die gleiche Pandemie der Ungeimpften, obwohl der Impfstoff gar nicht gegen diese nicht mit Corona zusammenhängenden Todesfälle wirkt. Demnach würde der Impfstoff gegen alles wirken, was aber völlig abstrus ist.
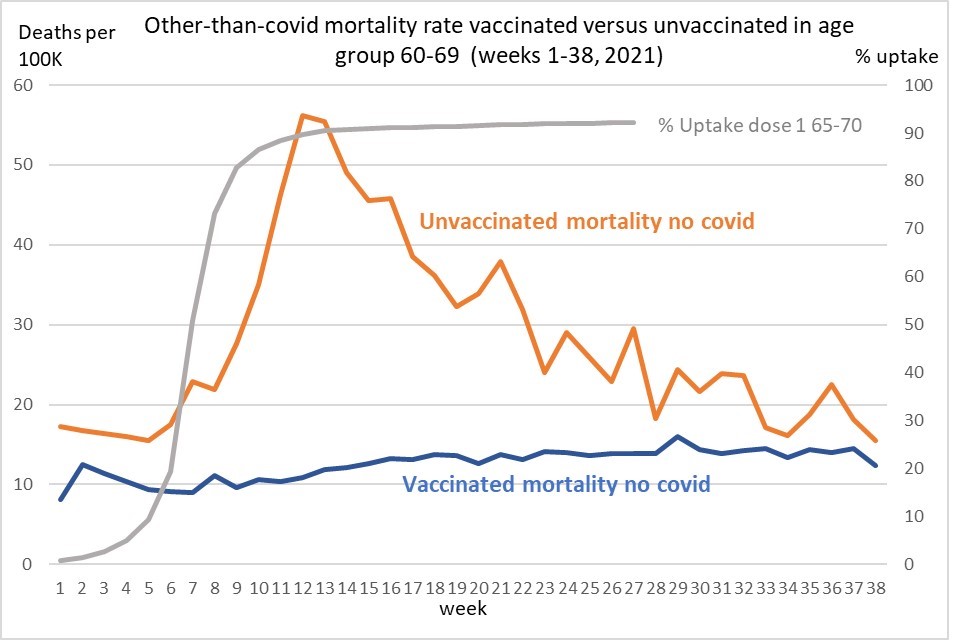
Abb. 2: Andere Mortalität im mathematischen Modell, Quelle.
Das klingt nach einer steilen These, wenn man die aktuelle Nachrichtenlage verfolgt. Ganz so steil ist sie aber gar nicht, wenn man die Studie von Whittaker et al. (2021) kennt. In dieser norwegischen Studie hat man keinen Unterschied in der Wahrscheinlichkeit auf einen Tod im Krankenhaus zwischen geimpften und ungeimpften Patienten entdeckt– hierbei geht es also um die wirklich schweren Fälle. Medial geframed werden die Ergebnisse dieser Studie meist mit dem Umstand, dass vollständig Geimpfte kürzere Krankenhausaufenthalte zeigten. Ziel des Impfstoffes war ja aber vor allem eine Reduzierung der individuellen Chance auf den Exitus.
Schaut man nun auf diese Studie, sind die Ergebnisse von Prof. Fenton nicht mehr so abwegig. Heißt das aber nun, dass der Impfstoff nicht wirkt? Das kann man mit dieser Modellrechnung freilich nicht beweisen. Allerdings stellt sie das Narrativ der Pandemie der Ungeimpften in Frage, wobei in der realen Welt dieser modellierte Effekt noch durch die Faktoren verstärkt wird, die bereits im vorangegangenen Artikel beschrieben wurden, (z.B. verstärktes Testen von Ungeimpften) aber nicht Teil der Modellrechnung hier sind beziehungsweise sein können.
Pandemie der ungeeigneten Daten
Man sieht bei dieser Simulation einmal mehr, wie unverlässlich die Daten eigentlich sind, auf denen Politik und Medien die Narrative fußen und wie leicht manipulierbar die Zahlen sind. In der Spieltheorie spricht man von einem so genannten Stufenspiel. Das bedeutet, dass in einer ersten Stufe Regeln festgelegt werden, die dann in der zweiten Stufe angewendet werden. Der entscheidende Punkt ist, dass sich ein Teil der Spieler plötzlich in Stufe 2 wiederfindet, ohne dass er die Regelsetzung in Stufe 1 mitbekommen hat. Im konkreten Fall hat die Regierung z.B. den Inzidenzwert in Stufe 1 als Entscheidungsgrundlage für weitere Maßnahmen festgelegt. Dieser wurde dann dem Parlament und den Bürgern als objektiver Wert verkauft. Näheres Hinsehen zeigt aber, dass dieser Wert gar nicht so objektiv ist. Er kann u.a. durch die Teststrategie zu einem gewissen Grad gesteuert werden. Das fällt dann auch irgendwann den anderen Spielern auf, aber die Regelsetzung ist ja bereits geschehen. Als, um beim Beispiel zu bleiben, die Inzidenz als Entscheidungsfaktor anerkannt wurde, hatten die anderen Spieler also bereits ‚verloren‘, ohne es zu merken.
Die Daten in Deutschland zum Beispiel, so wie in vielen Ländern auch, werden nicht unabhängig erhoben. Das Robert-Koch-Institut befindet sich im Geschäftsbereich des Bundesministeriums für Gesundheit, dem der Gesundheitsminister vorsteht, der diese Zahlen völlig unhinterfragt nutzt und verkauft, als seien sie perfekt und über jeden Zweifel erhaben. Die Modellrechnung zeigt einen möglichen Fallstrick.
„Es muss eine faire Datenerhebung geschehen, die solche Fallstricke vermeidet.“
Wer die Ungeimpften zu Sündenböcken machen will und ihnen grundlegende Rechte entziehen möchte, kann dieses Stufenspiel über Meldeverzögerung, über die Implementierung von Bias und weiteren Maßnahmen (überproportionales Testen von Ungeimpften, unterschiedliche Falldefinitionen etc.), spielen. Selbst bei einem völlig unwirksamen Impfstoff würde er noch die Ergebnisse bekommen, die er für die Politik braucht, um den Druck auf Ungeimpfte zu erhöhen.
Das ist eine Schwäche des aktuellen politischen Systems und wenn man für kommende Pandemien gerüstet sein will, muss man auch dafür sorgen, dass so eine Manipulation grundsätzlich überhaupt nicht geschehen kann. Es muss eine faire Datenerhebung geschehen, die solche Fallstricke vermeidet, indem man z.B. Effekte einer Meldeverzögerung herausrechnet. Sonst kann man nämlich aus allem eine Pandemie machen und aus allem einen wunderbar wirksamen Impfstoff. Das ist generell gefährlich.
Was wäre bei einem tödlicheren Placebo?
Dieses mathematische Phänomen unbeachtet zu lassen, was aktuell sehr offensichtlich geschieht, ist deshalb auch gefährlich, weil man dadurch einen Wirkstoff mit einer höheren Mortalitätsrate nicht erkennen würde – man sähe weiterhin eine Pandemie der Ungeimpften. Auch das kann man in einer Modellrechnung mit der gleichen Meldeverzögerung nachweisen. Bei einer Mortalität von 17 auf 100.000 unter den Geimpften nähern sich die Mortalitäten von Geimpften und Ungeeimpften zwar schneller einander an, aber die angebliche „Pandemie der Ungeimpften“ scheint nach wie vor über Wochen nachweisbar (wobei in der Realität natürliche Schwankungen die Sichtbarkeit einschränken können).
Eine höhere Mortalität bliebe unter dieser Gruppe von 1.000.000 Menschen innerhalb der 20 Wochen kaum an Grafiken identifizierbar, obwohl sie bestünde. Wenn man nun – etwa durch Booster – immer dasselbe wieder durchspielt, wird es anhand dieser Zahlen immer unerkannt bleiben, dass es nie eine „Pandemie der Ungeimpften“ gab und das Vakzin vielleicht sogar tödlicher ist als das ungeimpfte Leben – übrigens auch dann, wenn man den Faktor Tod etwa durch die Daten zu Hospitalisierungen oder positiven Tests austauscht. Es ergibt sich das gleiche Spiel.
Ohne Meldeverzug ist die Effizienz von einem Placebo gleich 0 – mit Meldeverzögerung sieht es anders aus. Bis Woche 12 kann man grandiose Erfolgsmeldungen bringen: das Placebo ist enorm effizient. Danach kracht die Effizienz ziemlich brutal ein, bleibt aber über 0. Diese Simulation (s. Abb. 3) wirkt wie eine Blaupause der in der realen Welt gemessenen Effizienz der Impfstoffe, die in den ersten Wochen angeblich tolle Ergebnisse erzielt und deren Effizienz dann nach und nach zerbröselte, wie hier beschrieben.
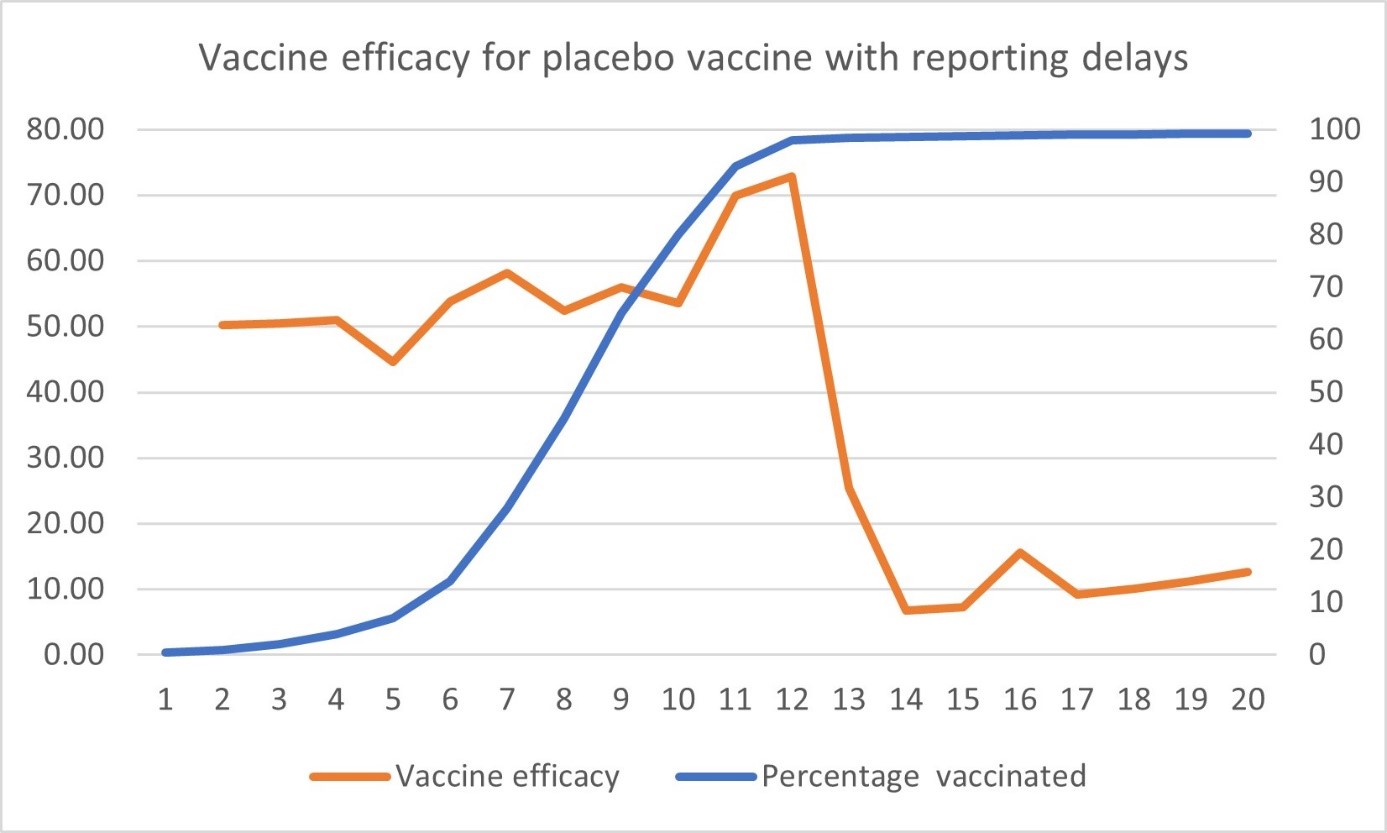
Abb. 3: Wirksamkeit im mathematischen Modell, Quelle.
Beweist das aber jetzt, dass die Corona-Impfstoffe gar nichts taugen? Nein. Es zeigt nur, dass die Datenlage nicht so klar und eindeutig ist, wie oft getan wird. Wenn man in einer Kontrollgruppe mit einem Placebo – und das simulieren diese Modellrechnungen – ähnliche Verläufe und Phänomene beobachtet wie mit einem echten Impfstoff, deutet das, dass die „Wirkung“ der Impfstoffe womöglich voreilig interpretiert werden. Somit ist die Moral von der Geschicht‘: So aussagekräftig wie gedacht sind die Daten nicht.